Axiomas de campo de los números reales

Los números reales se utilizan, técnicamente en todas las ramas de las matemáticas y es importante tener una noción sobre ellos antes de abordar los Axiomas de campo de los números reales. Se enunciarán las propiedades de los números reales: adición y producto, y el significado de estos números. Toma en cuenta que los axiomas se consideran como verdaderos, no se demuestran, sólo se aceptan.

¿Qué son los números reales?

Prácticamente los números reales son un conjunto de números con propiedades heredadas. Es decir, este conjunto se puede construir o definir a través de la existencia de los número racionales, y definiendo luego un número real en términos de números racionales. Este es método usado por Dedeking. Es un conjunto denso, quiere decir que siempre existirá un número real entre otros dos.

Se definen dos relaciones, también llamadas operaciones, en el conjunto de los números reales: la suma o adición y la multiplicación o producto. Es conocido que la resta es un caso particular de la adición, y que la división es un caso particular del producto. Los axiomas considerados son: axiomas de campo y axiomas de orden.

Símbolo de los números reales

El conjunto se denota por $\mathbb{R}$ y se compone, como se mencionó, de otros conjuntos.

Composición de los números reales

Números naturales: son los números que nos sirven para contar y ordenar, se simboliza por $\mathbb{N}$ y se puede expresar por:

$\begin{align*} \mathbb{N} = \{1,2,3,4,...\} \end{align*}$

Algunos autores consideran el número $0$ como parte de los números naturales, no es una regla.

Números enteros: es conjunto se compone de los números naturales, sus negativos y el cero, y el símbolo para denotarlo es $\mathbb{Z}$ , la notación para este conjunto es

$\begin{align*} \mathbb{Z} = \{...,-4,-3,-2,-1,0.1,2,3,4,...\} \end{align*}$

Números racionales: cada elemento de este conjunto se expresa de la siguiente forma $p/q$ , donde $p$ y $q$ son son números pertenecientes a los enteros y $q$ siempre es distinto de cero. Tienen una expansión decimal infinita o periódica. Se denota con la letra $\mathbb{Q}$ :

$\begin{align*} \mathbb{Q} = \{p/q : p \ \text{y} \ q \in \mathbb{Z} \ \text{y} \ q \neq 0 \} \end{align*}$

Números irracionales: Son números que no pueden escribirse de la forma $p/q$ , tienen una expansión decimal infinita y apreiódica. El conjunto se denota por $\mathbb{I}$ . Ejemplo de ellos es el número $\pi$

La unión de los conjuntos anteriores forman al conjunto de los números reales.

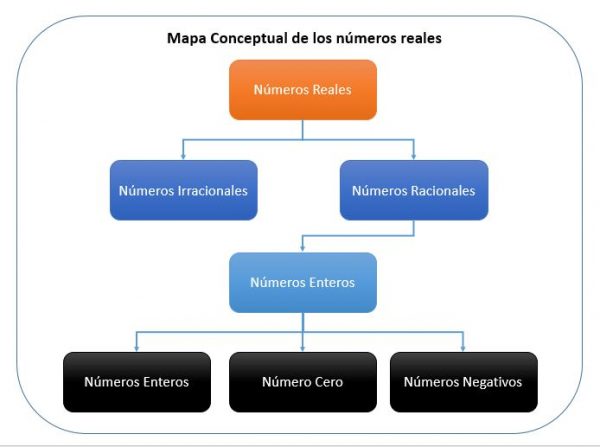
Mapa Conceptual de los Números Reales

Una forma de entender el sistema de los números reales, es a través de un mapa conceptual, que va desde el nivel primario o base, hasta el conjunto de reales.

Mapa conceptual de los números reales

Axiomas de campo de los números reales

En el conjunto de los número reales, se definen dos operaciones: la suma o adición y el producto o multiplicación y una relación de orden, denotada por “<” que satisfacen los siguientes axiomas. A estos axiomas también se les conoce como propiedades de los números reales.

Axiomas de la adición

Axioma 1 Para todo $a$ y $b$ en $\mathbb{R}$ , $a+b \in \mathbb{R}$ . Estabilidad o cerradura. Se dice que los números reales son cerrados respecto a la adición (escrita frecuentemente por +). Esto quiere decir que a cada par de números en este conjunto, por ejemplo, $a$ y $b$ corresponde exactamente un número real $a+b$ . Llamado suma de $a$ y $b$ .

Axioma 2 Para todo $a$ y $b$ en $\mathbb{R}$ , $a+b = b+a$ . Ley conmutativa.

Axioma 3 Para todo $a$ , $b$ y $c$ en $\mathbb{R}$ , $(a+b) +c = a + (b+c)$ . Ley asociativa.

Axioma 4 Existe un elemento y sólo uno, al que se denota por “0”, tal que para todo $a$ en $\mathbb{R}$ , $a+0=a=0+a$ . La existencia y unicidad del elemento neutro aditivo.

Axioma 5 Para cada $a$ en $\mathbb{R}$ , hay un y sólo un elemento, al que se denota por $-a$ , tal que $a+(-a) = -a+a$ . La existencia y unicidad del elemento inverso aditivo.

Axiomas de la multiplicación

Axioma 1 Para todo $a$ y $b$ en $\mathbb{R}$ , $ab \in \mathbb{R}$ . Estabilidad. Este conjunto también es cerrado en relación a la multiplicación (escrita por conveniencia por $\cdot$ ), equivalentemente a cada par de números $a$ , $b$ corresponden un número real $a \cdot b$ también escrito como $ab$ , llamado producto de $a$ y $b$ .

Axioma 2 Para todo $a$ y $b$ en $\mathbb{R}$ , $ab = ba$ . Ley conmutativa.

Axioma 3 Para todo $a$ , $b$ y $c$ en $\mathbb{R}$ , $(ab) c = a (bc)$ . Ley asociativa.

Axioma 4 Existe un elemento y sólo uno, al que se denota por “1”, diferente de “0”, tal que para todo $a$ en $\mathbb{R}$ , $a \cdot 1=a=1 \cdot a$ . La existencia y unicidad del elemento neutro multiplicativo.

Axioma 5 Para cada $a$ en $\mathbb{R}$ , hay un y sólo un elemento, al que se denota por $a^{-1}$ , tal que $a \cdot a^{-1} = 1 = a^{-1} \cdot a$ . La existencia y unicidad del elemento inverso multiplicativo.

Axioma distributivo

Axioma Para todo $a$ , $b$ y $c$ en $\mathbb{R}$ , $a(b+c)=ab+ac$ y $(b+c)a=ba+ca$ . Ley distributiva.

Axiomas de orden

Axioma 1 Para cualesquiera dos elementos $a$ y $b$ en $\mathbb{R}$ , una y sólo una de las sigueintes relaciones se verifica: $a<b$ , $a = b$ , $b < a$ Ley de tricotomia.

Axioma 2 Si $a<b$ y $b<c$ , entonces $a<c$ . Ley transitiva.

Axioma 3 Si $a<b$ , entonces, para todo $c$ en $\mathbb{R}$ , $a+c<b+c$ .

Axioma 4 Si $a<b$ y $0<c$ , entonces $ac<bc$

Axioma fundamental

Existe un conjunto que se denota por $\mathbb {R}$ que satisface los tres tipos de axiomas mencionados, de orden, algebraicos y topológicos.

Referencias

Haaser, La Salle y Sullivan. Análisis Matemático Tomo 1. Editorial Trillas.
Bartle y Sherbert. Introducción al Análisis Matemático de una variable. Limusa Wiley.

¿Qué son los números reales?

Símbolo de los números reales

Composición de los números reales

Mapa Conceptual de los Números Reales

Axiomas de campo de los números reales

Axiomas de la adición

Axiomas de la multiplicación

Axioma distributivo

Axiomas de orden

Axioma fundamental

Referencias

Deja un comentario Cancelar respuesta