Teoría de conjuntos: conceptos, sus símbolos y construcción

Empezaremos con una Introducción a la Teoría de conjuntos. Con especial tratamiento, para diferenciar lo que es una colección o clase de un conjunto. Esencialmente se intenta esclarecer que todo conjunto es una clase y no a la inversa. Se presentarán algunos teoremas básicos. Como también el álgebra de conjuntos: relaciones, par ordenado, particiones y funciones.

Contenido

Definición de conjunto

Se dice que un conjunto es una colección de objetos. Se puede entender que el conjunto está constituido por una multiplicidad de objetos, y estos a la vez se consideran una unidad. A los objetos suele llamárseles elementos del conjunto. Prácticamente todo objeto puede llegar a formar un conjunto, por ejemplo, un conjunto de conjuntos, todos objetos, excepto las colecciones.

Lo que estudia la teoría de conjunto son los objetos que pertenecen a estos. Se cumplen los siguientes postulados:

Si 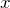$x$ no tiene elementos, entonces 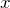$x$ es un objeto que estudia la teoría de conjuntos.
Si 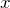$x$ es un conjuntos, entonces es un objeto que estudia la teoría de conjuntos.
Los únicos objetos de la teoría de conjuntos son antes descritos en los incisos 1 y 2.

Ejemplo de conjuntos

El conjunto de los colores del arcoíris. Se consideran siete colores: rojo, naranja, amarillo, verde, turquesa, azul, y violeta (morado).

Las vocales: a, e, i, o, u.

Los números arábigos: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9

Conjuntos por extensión

Es posible escribir los conjuntos anteriores como

A = {rojo, naranja, amarillo, verde, turquesa, azul, violeta }

V = {a, e, i, o, u}

N = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}

A esto se le suele llamar conjuntos por extensión, la cual enumera o nombra los elementos de un conjunto. El conjunto va entre llaves, y sus elementos se separan por comas.

Conjuntos por compresión

Los conjuntos se escriben en términos de una característica.

A = {a | a es un color del arcoíris}

V = {v | v es una vocal}

N = {n | n es un número arábigo}

Más adelante hablaremos de la propiedad de un conjunto, y se mostrarán ejemplos de conjuntos infinitos. En los conjuntos mencionados, existen símbolos, conviene conocerlos, por lo que en la siguiente párrafo veremos cuáles son y su descripción.

Símbolos utilizados en la Teoría de conjuntos

Los símbolos que frecuentemente son utilizados para hablar de conjuntos son los siguientes: para todo ( $\forall$ ), existe ( $\exists$ ), igual o identidad (=), variables u objetos individuales ( $x_1, x_2, x_3, ...$ ). Símbolo de pertenencia ( $\in$ ), no pertenencia ( $\not\in$ ). En general la negación particulares símbolos, se identificará con una raya que lo atraviesa desde arriba, hasta abajo, por la mitad.

Símbolo	Descripción
{}	Las llaves (abrir y cerrar) se usan para referirse a un conjunto y delimitar sus elementos. Por ejemplo el conjunto vacío {}, el conjunto de los primeros 5 números naturales {1,2,3,4,5}
∈	Para indicar si un objeto pertenece al conjunto.
∉	Para indicar si un objeto no pertenece al conjunto.
\|	Se llama pipe o barra vertical, se usa en lugar de las palabras “tal que”.
n (C)	Cardinalidad del conjunto C. La letra C, puede variar: A, B, recordar que las mayúsculas se usan para representar conjuntos.
U	Conjunto Universo.
Φ	Conjunto Vacío. También son usados las llaves {}, el símbolo $\emptyset$ para el vacío.
⊆	“Subconjunto de”, también como “es un conjunto de”, es decir, el conjunto se considera elemento de otro conjunto
⊂	Subconjunto propio de, también como “es un conjunto propio de”, es decir, el conjunto se considera elemento de otro conjunto
∩	Intersección de conjuntos.
∪	Unión de Conjuntos.
‘	(A’ ) Complemento del conjunto A. También se usa la línea arriba $\overline{A}$
…	Los elementos del conjunto, continúan
$a \implies b$	Entonces. Si “a” entonces “b”
⇔	Si y sólo si.
∼	No (negación). También se usa $\neg$
∧	Y, conjunción.
∨	O, disyunción.

Considérese el caso para decir que dos objetos son iguales, contra el caso donde un objeto pertenece a otro. La afirmación para la igualdad estará dada por $x=y$ , mientras que la pertenencia por $x\in y$ . La escritura de cada afirmación será determinada por una propiedad.

Propiedad de un conjunto

Una propiedad es una afirmación, que se refiere a la manera en que los objetos que forman un conjunto. Por ejemplo si deseáramos decir que existe un conjunto que tiene un elemento podemos escribir $\exits a (a \in A)$ . Denote al conjunto por A (mayúscula) porque varios autores se refieren a los conjuntos por letras mayúsculas, mientras que a sus elementos por minúsculas.

Se puede percibir que todo conjunto está determinado por una propiedad. Para todo conjunto $A$ , existe una propiedad $P$ tal que:

$\begin{align*} a \in A \Leftrightarrow a \text{ cumple } P. \end{align*}$

Es posible abreviar esta expresión de la siguiente forma:

$\begin{align*} \{ a \mid a \text{ cumple } P \} \end{align*}$

Es decir, el conjunto de objetos $a$ que cumple la propiedad $P$ .

Conjunto vacío

El conjunto que no tiene elementos, recordemos que se denota por el símbolo $\emptyset$ , es el conjunto vacío. Entonces, su propiedad es: el conjunto sin elementos. El conjunto vacío se definirá por:

$\begin{align*} \emptyset = \{ x \mid x \neq x \} \end{align*}$

Aunque parece se no clara la definición del conjunto vacío, lo que se dice es, un elemento llamado $x \in \emptyset$ no es igual así mismo. El resultado será que ningún objeto cumplirá esta propiedad. De esta manera se define al conjunto vacío.

Hay una particularidad que resaltar. si existe la posibilidad de que objectos no sean conjuntos, por ejemplo $y$ , entonces existirá un conjunto sin elementos que será diferente del vacío. Es decir, el conjunto vacío no es igual al conjunto sin elementos.

¿Qués es una colección?

Una colección o también llamada clase es, la manera de referirnos a todos los objetos que cumplen una propiedad. Es decir:

$\begin{align*} C = \{ x \mid x \text{ cumple la propiedad } P \} \end{align*}$

De tal forma que la expresión “ $x \in C$ ” es otra forma de decir que “ $x$ cumple la propiedad $P$ “. Se puede concluir que que todo conjunto es una colección o clase de objetos determinada por una propiedad. Mientras que la afirmación inversa, no necesariamente se cumple: que toda clase sea un conjunto.

Observaciones

Los objetos que constituyen un conjunto, se les conoce como los elementos del conjunto. Un conjunto puede ser un elemento de un conjunto.
La pertenencia es una relación de los elementos con el conjunto. Una relación no es una propiedad.
La relación 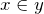$x \in y$ es cierta, se entiende que 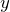$y$ es un conjunto, mientras que x puede o no serlo.

Construcción de conjuntos

Entiéndase que la construcción de conjuntos está basada en procedimientos empíricos, mentales, serán verdades dadas, sin necesidad de demostrarlas. Este procedimiento es intuitivo y hasta cierto punto, personal. Veamos la construcción de un conjunto:

Axioma del conjunto vacío

Este conjunto es posible construirlo sin usar objetos, o elementos. Se conoce como el conjunto vacío. ¿Cómo se ha construido? Sencillamente se determinó un propiedad: el conjunto sin elementos. Esa imagen que nos queda en la mente, es la que le da vida. Para, por decirlo de alguna forma, materializarlo, se simboliza con $\emptyset$ . Así de simple.

Axioma del Par

Dados dos objetos A y B, se puede construir el conjunto que contienen estos dos elementos y sólo estos dos. El cual se denota por {A,B} y se le llama el par de A y B. Un caso particular de este axioma es el conjunto cuyo único elemento es A, el cual escribimos como {A} al que se le llama el unitario de A (caso en el que A=B). Para cualquier número n finito de objetos $A_1, A_2,...,A_n$ es posible construir el conjunto

$\begin{align*} \{ A_1, A_2,...,A_n \} \end{align*}$

Subconjunto

Sean $A$ , $B$ dos conjuntos, $A$ es un subconjunto de $B$ si todos los elementos de $A$ también es elemento de $B$ . El cual se denota por $A \subseteq B$ . Es decir,

$\begin{align*} \forall x (x \in A \Rightarrow x \in B ) \end{align*}$

Si dos conjuntos tienen los mismos elementos, entonces, estos conjuntos serán iguales. También podemos decir que es el mismo conjunto, con diferente nombre.

$\begin{align*} A \subseteq B \text{ y } B \subseteq A \end{align*}$

Clases de conjuntos

Se puede dar una clasificación de los conjuntos, estos pueden ser homogéneos y heterogéneos; orenables y no ordenables finitos e infinitos. Si al comparar dos conjuntos se puede determinar si son o no iguales; además si son coordinables o no.

Conjuntos Homogéneos y Heterogéneos

Es homogéneo un conjunto cuando los elementos que lo integran son de la misma especia. Y heterogéneos cuando son de diferente especie.

Conjuntos ordenables y no ordenables

Es posible establecer un criterio de ordenación, de tal forma que permita determinar la posición de un elemento en relación a otro dentro del mismo conjunto, si es posible esto, se dice que es ordenable. Ejemplo de ellos es el conjunto de los números naturales.

Si no se puede establecer un criterio de ordenamiento, entonces el conjunto es no ordenable.

Conjuntos finitos e infinitos

En palabras sencillas se dice que es finito si se puede contar. Es decir, que el número de elementos tenga un límite $n$ . Es infinito si no es finito. Así de sencillo, puede decirse que si es incontable, entonces es infinito. Es decir, si siempre existe un número que sea mayor al límite. Los puntos en la recta, es un conjunto infinito.

2 comentarios en «Teoría de conjuntos»

RAÚL

15 junio, 2021 a las 1:58 am

Excelente información, seguir brindando
Responder
Carmen

21 octubre, 2023 a las 2:27 pm

Muchas gracias, me ayudaste mucho. Felicitaciones
Responder

Deja un comentario Cancelar la respuesta

Este sitio usa Akismet para reducir el spam. Aprende cómo se procesan los datos de tus comentarios.